Bezier曲线与Catmull-Rom曲线

2022-09-04

Bezier曲线（贝塞尔曲线）

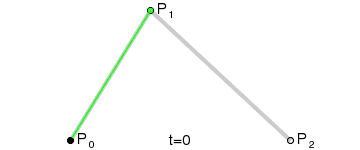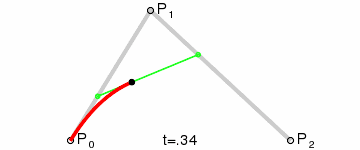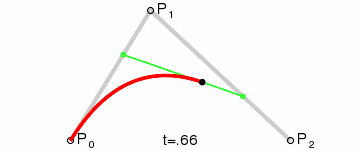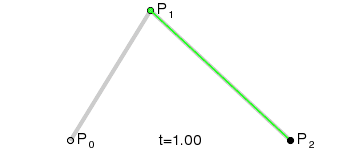
贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。

公式：
贝塞尔公式

图解：
贝塞尔图解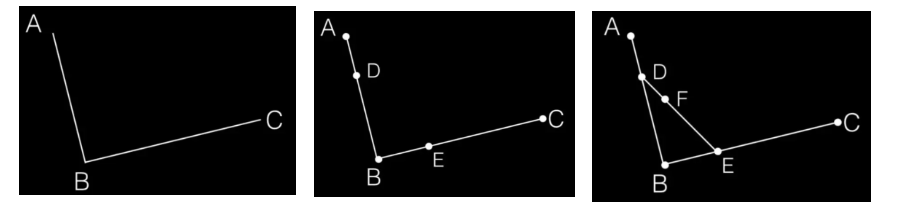
DF:DE = AD:AB = BE:BC

N阶贝塞尔曲线

ｎ个控制点对应着ｎ－１阶的贝塞尔曲线，并且可以通过递归的方式来绘制。
一阶曲线:
一阶贝塞尔

二阶贝塞尔:
常见的贝塞尔曲线便是二阶。

三阶贝塞尔: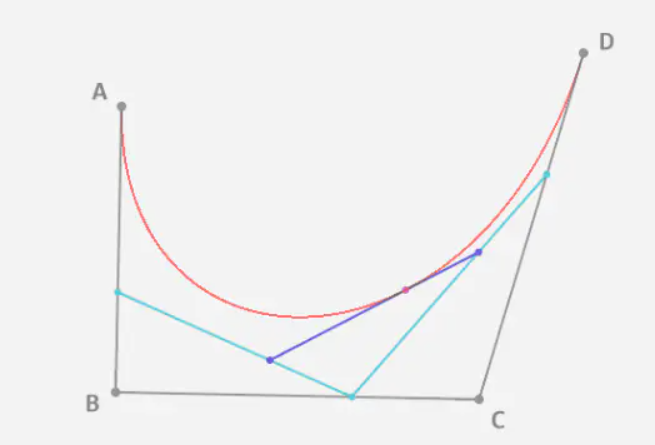

贝塞尔曲线的性质

1 各项系数之和为1.
系数是二项式的展开(t+(1-t))^n = (1)^n非负性，二项式的展开。
2 对称性
第i项系数和倒数第i项系数相同, 从二项式的展开来思考,这个也好理解。
3 递归性
我们就是从递归来理解贝塞尔曲线的。
4 凸包性质
贝塞尔曲线始终会在包含了所有控制点的最小凸多边形中, 不是按照控制点的顺序围成的最小多边形. 这点大家一定注意.　这一点的是很关键的，也就是说可以通过控制点的凸包来限制规划曲线的范围，在路径规划是很需要的一个性质．５端点性质第一个控制点和最后一个控制点，恰好是曲线的起始点和终点．这一点可以套用二项式展开来理解，ｔ＝１或者０的时候，相乘二项式的系数，出了初始点或者末尾点，其余的都是０
６一阶导数性质

代码实现

U3D中C#的实现：

public static Vector3 CreateBezierCurvePoint(Vector3 beginPos, Vector3 controlPos, Vector3 endPos, float t)
{
    return Mathf.Pow(1 - t, 2) * beginPos + 2 * t * (1 - t) * controlPos + Mathf.Pow(t, 2) * endPos;
}
public void GeneratePoints()
    {
        //暂时因为在Update中生成曲线节点，所以每次生成前清空节点列表
        nodeList.Clear();

        //如果5个节点 将分成4个部分
        float ratioInterval = 1 / (nodeCount - 1);

        float t = 0;
        //根据节点数量生成坐标
        for (int i = 0; i < nodeCount; i++)
        {
            Vector3 pos = CreateBezierCurvePoint(beginTF.position, controlTF.position, endTF.position, t);
            nodeList.Add(pos);
            t += ratioInterval;
        }
    }

Catmull-Rom曲线

有时候我们想要物体从一个点移动到另一个点，但并不希望它沿着直线移动过去，而是稍微弯曲一点，这时候catmull-rom样条就派上用场了。
通过4个控制点确定一条曲线，曲线必通过中间两控制点。
原理啥的…暂时学不动了，有闲暇时间再补上吧。

代码实现

贴一个U3D中C#的实现：

Vector3 CatmullRomPoint(Vector3 P0, Vector3 P1, Vector3 P2, Vector3 P3, float t)
{
    float factor = 0.5f;
    Vector3 c0 = P1;
    Vector3 c1 = (P2 - P0) * factor;
    Vector3 c2 = (P2 - P1) * 3f - (P3 - P1) * factor - (P2 - P0) * 2f * factor;
    Vector3 c3 = (P2 - P1) * -2f + (P3 - P1) * factor + (P2 - P0) * factor;

    Vector3 curvePoint = c3 * t * t * t + c2 * t * t + c1 * t + c0;

    return curvePoint;
}