3D数学

坐标系

左手坐标系与右手坐标系

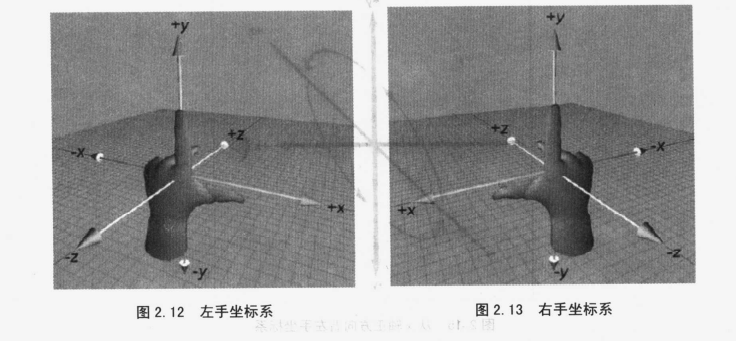
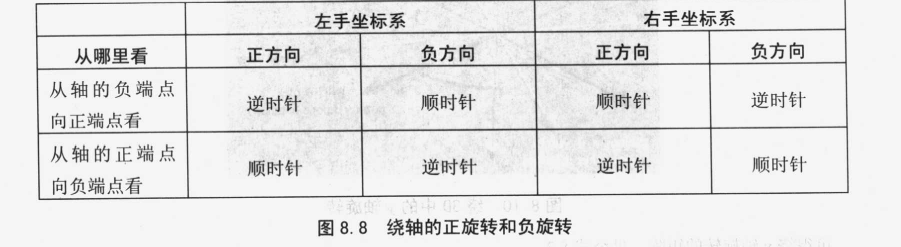
绕轴旋转时，必须知道哪个方向是“正”，哪个方向是“负”：
左手坐标系：
左手法则：伸出左手，大拇指向上，其余四指弯曲。大拇指指向旋转轴的正方向，此时四指弯曲的方向就是旋转的正方向。
右手坐标系：
相反。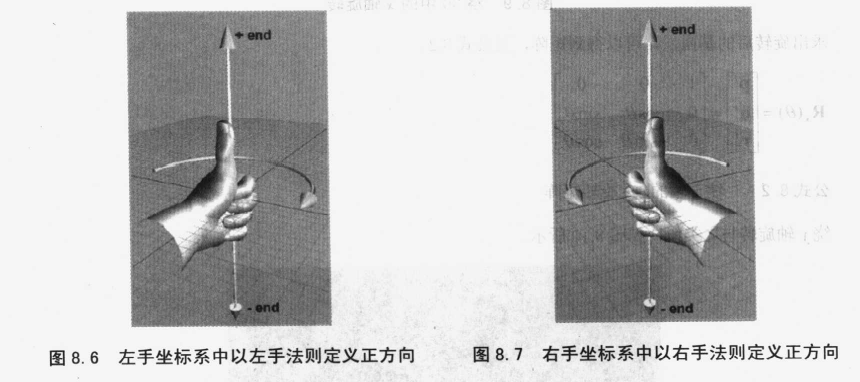

一些重要的坐标系

• 世界坐标系
• 物体坐标系
• 摄像机坐标系
  

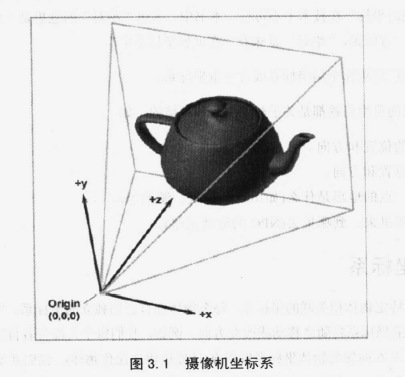
惯性坐标系

引入惯性坐标系，是为了简化世界坐标系到物体坐标系的转换，意思是世界坐标系到物体坐标系的“半途”。
惯性坐标系的原点与物体坐标系的原点重合，但轴平行于世界坐标系的轴。
物体坐标系转惯性坐标系只需要旋转，然后惯性坐标系转世界坐标系只需要移动。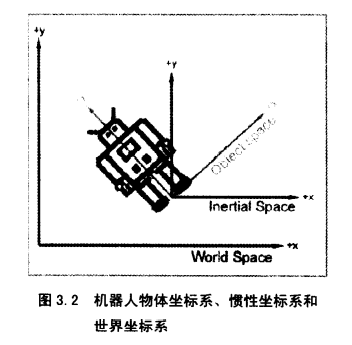

坐标系转换

解决问题：知道某一点的坐标，如何从另一个坐标系去描述这个点？
方法：

• 将轴从物体坐标系转为世界坐标系

1. 将物体旋转到惯性坐标系
2. 将惯性坐标系平移到世界坐标系

注：站在物体本身的角度来看，旋转和平移的方向相反

3D中的方位与角位移

方向与方位

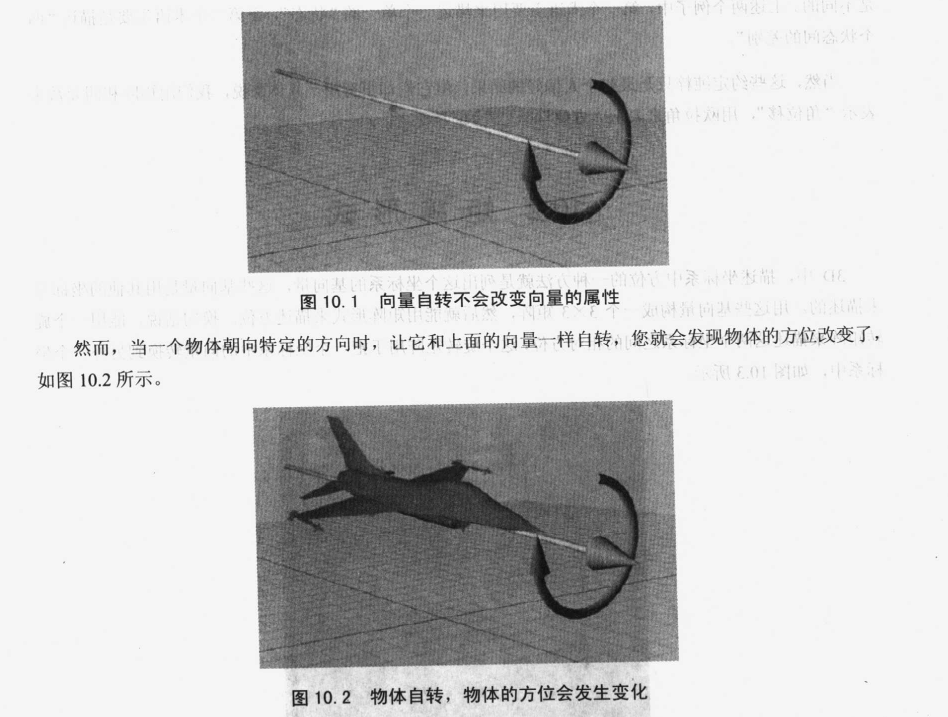
从技术角度来讲，这就说明在3D中，只需要两个数字就能表示一个方向，但是要确定一个方位，却需要三个数字。

描述位置：相对于坐标系原点的偏移。
描述方位：相对于已知方位的旋转来描述的，旋转的量称为角位移。

表示方位：矩阵形式

用一个旋转矩阵来描述两个坐标系之间的相对方位，这个旋转矩阵用于把一个坐标系中的向量转换到另外一个坐标系中。

优点：

1. 可以立即进行向量的旋转
2. 矩阵的形式被图形API所使用
3. 多个角位移连接：可以解决嵌套坐标系
4. 矩阵的逆：就是“反”角位移，旋转矩阵是正交的

缺点：

1. 占用了更多的内存
2. 难以使用
3. 矩阵可能是病态的：矩阵的9个数可能只有3个数是必须的，会造成冗余。行必须是单位向量，且它们必须互相垂直。

表示方位：欧拉角形式

欧拉角的基本思想就是将角位移分解为绕3个互相垂直的三个旋转组成的序列。

哪三个轴？按什么顺序？任意三个轴，任意顺序都可以。
但最常用的便是：“hedaing-pitch-bank”约定，它的基本思想是让物体开始于“标准”方位——即物体坐标系与惯性坐标系对齐，随后让物体做旋转，达到我们想要描述的方位。
（左手坐标系）
hedaing：+y向上
pitch：+x向右
bank：+z向前

示例：

1. 物体坐标系与惯性坐标系重合
2. 绕y轴（hedaing）
3. 绕x轴（物体坐标系的x轴）（pitch）
4. 绕z轴（物体坐标系的x轴）（bank）

优点：

1. 容易使用
2. 表达方式简洁
3. 任意三个数都是合法的

缺点：

1. 给定方位的表达方式不唯一
2. 求插值困难
3. 万向节死锁

表示方位：四元数

略

几何图元

表示方法

隐式表示：
通过定义一个bool函数f(x,y,z)，我们能够隐式表示一个图元。如果所指定的点在这个图元上，函数返回值为True。

参数形式表示：
…

“直接”形式表示：
自由度：每个几何图元都有的固有属性，自由度是无歧义描述该实体所需信息的最小数目。

直线和射线

一、两点表示法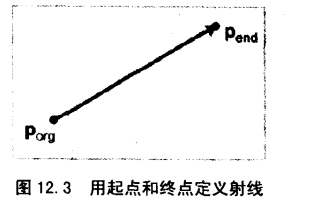

AABB

AABB是一个3D矩形，需要一个最大点和最小点。

可以用下面的类表示AABB：

class AABB{
public:
    Vector3 min;
    Vector3 max;
}

计算AABB：
计算一个顶点集合的AABB是非常简单的，先定义：

Vector3 min = MAXVALUE；
Vector3 max = MINVALUE；

随后，再遍历全部点，扩展边界：

if(p.x < min.x) min.x = p.x;
if(p.x > max.x) max.x = p.x;

其它以此类推。

变换AABB：
当物体移动/旋转时，AABB也需要随之变换。
通过变换AABB进行计算比通过物体再次计算AABB快得多。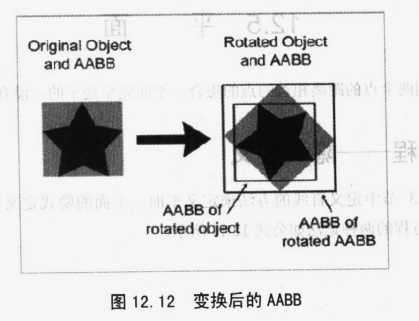

…待补充

赏

谢谢你请我吃糖果