图形学中的基本变换
二维变换
缩放变换
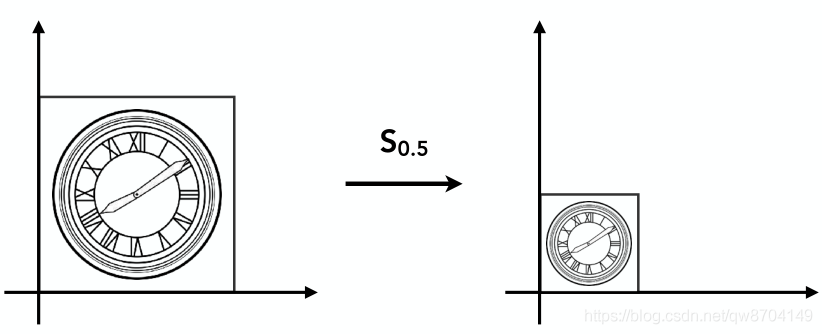
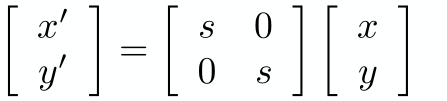
镜像变换
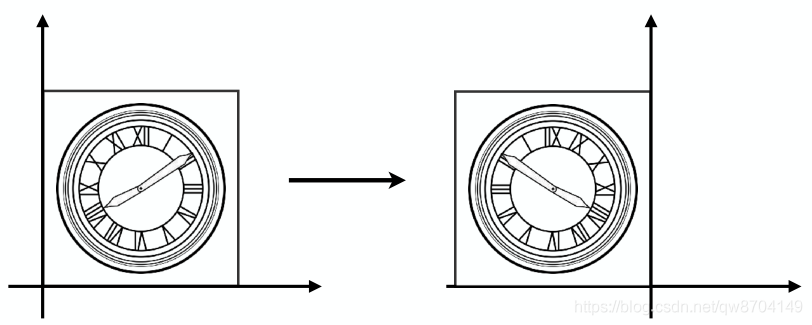
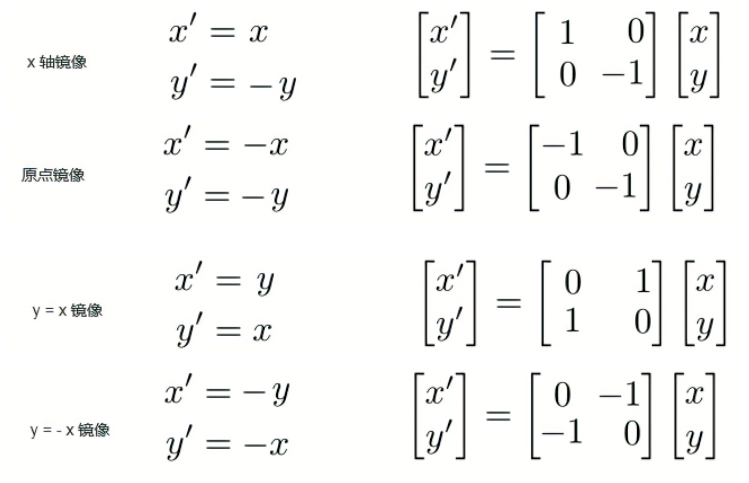
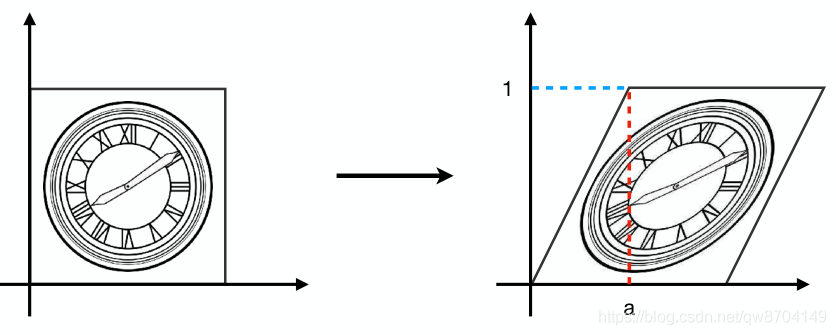
剪切变换
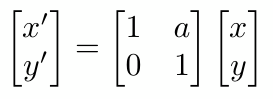
旋转变换
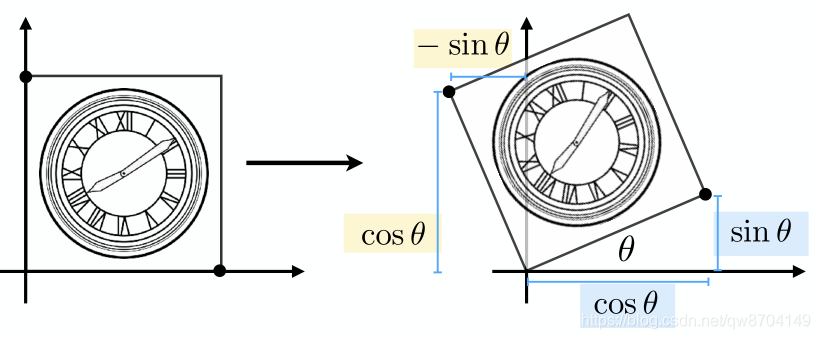
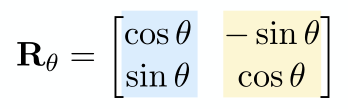
旋转矩阵是正交矩阵!
平移变换
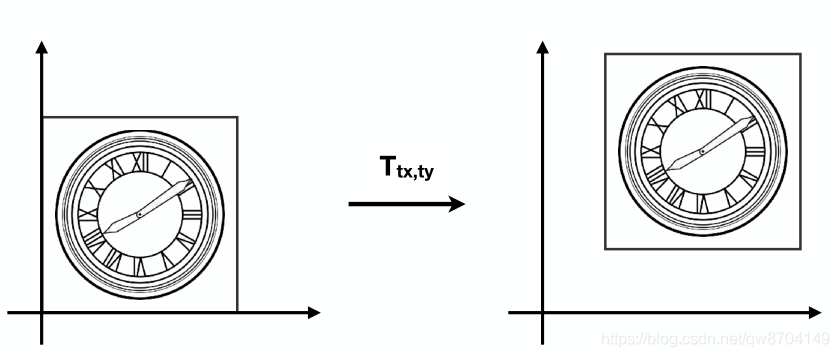
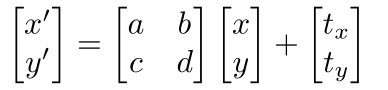
为了让平移变换也能只用一个矩阵表示,引入了齐次坐标:
故,公式变为:
逆变换
一个物体做一个变换,变换完以后要恢复到原来的位置,变换回原来的位置的过程称为逆变换,逆变换在数学上的实现是乘以变换矩阵的逆矩阵
组合变换
组合变换就是对一个物体进行多个变换,例如同时进行平移和旋转变换
非原点的旋转变换:移动到原点,旋转,再移动回原处
刚体变换
只有平移和旋转组成的变换称为刚体变换。
刚体变换的本质是一个物体的位置和角度发生了变换,物体本身的形状并不发生任何变化。
三维变换
平移变换
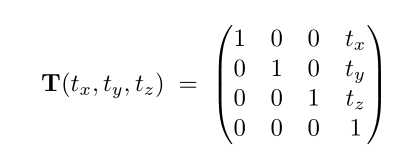
缩放矩阵
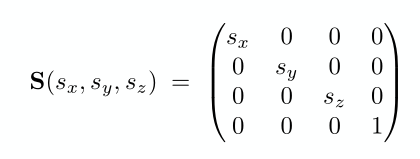
旋转矩阵
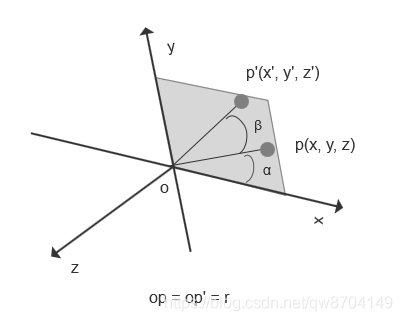
如上图,若有一点p在x轴和y轴所在平面上,p到到原点o的距离为r,即op=op’=r。
推导过程:
x = cos(α)*r
y = sin(α)*r
x’ = cos(α+β)*r
= (cos(α)*cos(β) - sin(α)*sin(β))*r
= (cos(α)*r)*cos(β) - (sin(α)r)sin(β)
= xcos(β) - ysin(β)
y’ = sin(α+β)*r
= (sin(α)*cos(β) + cos(α)*sin(β))*r
= (sin(α)r)cos(β) + (cos(α)r)sin(β)
= ycos(β) + xsin(β)
= xsin(β) + ycos(β)
转为矩阵表达: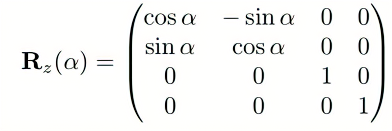
同理,绕x轴: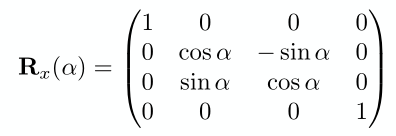
绕y轴: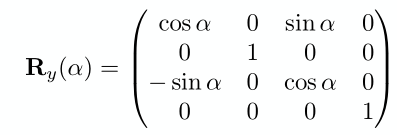
绕任意轴旋转:
基变换(补充)

MVP矩阵推导
左手坐标系:Unity采用左手坐标系。z轴代表前后,x轴代表左右,y轴代表上下。
右手坐标系:3dsMax采用右手坐标系。y轴代表前后,x轴代表左右,z轴代表上下。
Model Transformation
目标:
物体顶点的坐标:模型坐标系->世界坐标
M矩阵求法:
按照 缩放——旋转——平移 的顺序进行矩阵变换,因为这种结果是我们需要的。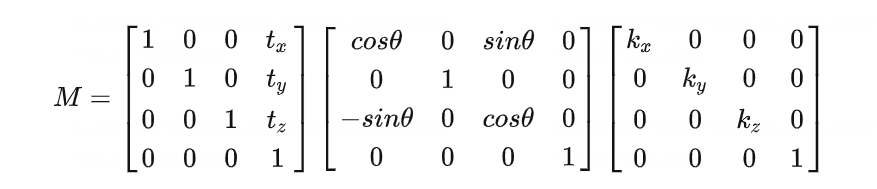
View / Camera Transformation
目标:
View矩阵是想把所有顶点从世界坐标系变换到以相机视角下的坐标系
求法:
Project Transformation
目标:把视野中的所有顶点摆放到[-1,1]标准立方体中
正交投影:
通过相机的参数可以确定视锥体(在正交投影下是一个长方体)在坐标系中的范围,定义在 x 轴上范围是[l,r],在 y 轴上范围是[b,t],在 z 轴上范围是[n,f]。我们要把这个长方体变换成标准立方体,需要先把长方体中心平移到原点,然后在 x,y,z 三个方向上进行放缩即可。于是有: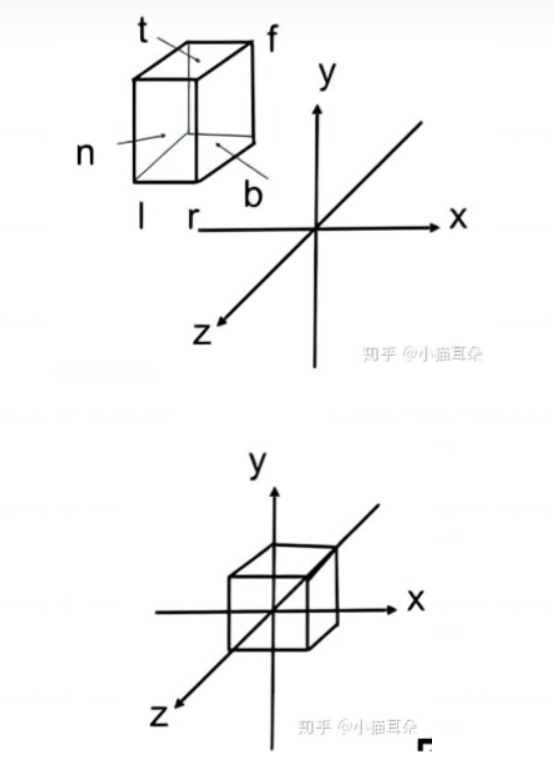
- 平移,计算出长方体的中心点为[(l+r)/2,(b+t)/2,(f+n)/2],然后将中心点移动到原点,矩阵为
- 缩放,例如从[l,r]缩放到[-1,1],缩放系数为2/(r-l)
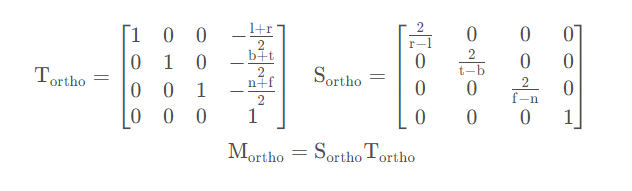
透视投影:
透视投影矩阵的视锥体是一个四棱锥的一部分,其中近平面为z=n,远平面为z=f,我们要把这个视锥体转换到一个正方体[-1,1][-1,1][-1,1]中,可以先把远平面压缩,把视锥体压缩成一个长方体,然后再通过第二步中的正交投影矩阵就可以变换到正方体中,如图: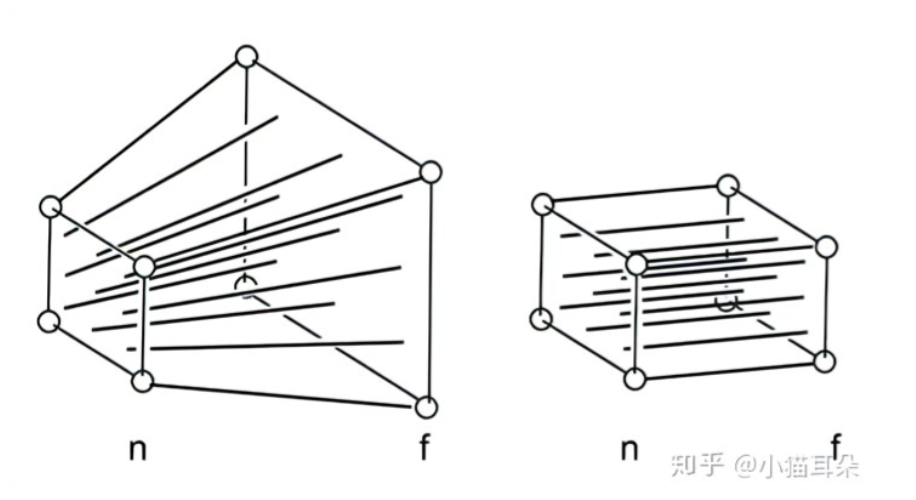
在把视锥体压缩成长方体的过程中,我们规定三个原则
- 近平面的所有点坐标不变
- 远平面的所有点坐标z值不变 都是f
- 远平面的中心点坐标值不变,为(0,0,f)
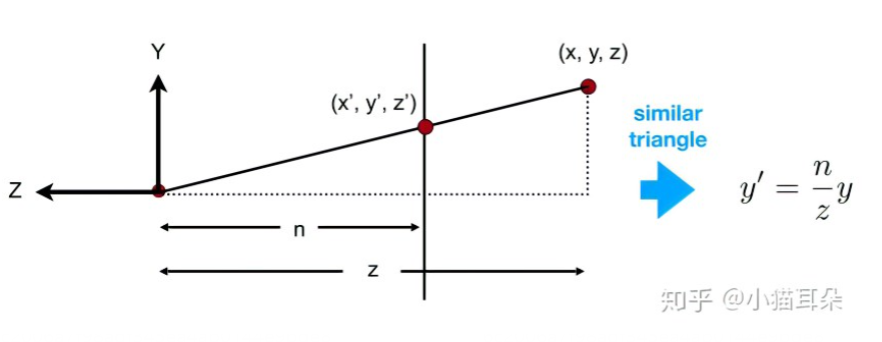
然后我们假设视锥体内的任意一点(x,y,z),压缩以后的xy坐标应该与近平面上对应的点相同,如图解相似三角形可以得到 y->ny/z x->nx/z
故对于(x,y,z,1)一点,它在视锥体压缩以后坐标应该为(nx/z,ny/z,unknow,1)。
也就是我们现在需要找到一个矩阵Mpersp->ortho,使得上面的转换成立。
假设矩阵的第一行为A,B,C,D。可以得到等式Ax+By+Cz+D = nx/z。
然后我们发现这个等式好像很难求,如果让A = n/z,其他等于0,的确可以得到结果。
但是矩阵的值应该是常数,n/z是个变量。
而其他的结果也很难写出来,同时矩阵的第二行也会有同样的问题 Ex+Fy+Gz+H = ny/z,也很难求。
所以我们换一种方法,前面根据已学知识可以知道(x,y,z,1)与(kx,ky,kz,k!=0)这两个点是完全等价的点,
所以我们让k取z可以把坐标(nx/z,ny/z,unknow,1)变为(nx,ny,still unknow,z)。
待续…
